6 spezifische Wärme und spezifische Wärmekapazität
Zunächst einige Beispiele um das Problem zu verdeutlich:
a) Zusammenhang zwischen Q und ΔT
Häufig wird die Wärmemenge mit der Temperatur verwechselt. Stoffe (wie beim ersten Beispiel der Kupferklotz) besitzen eine gewisse Wärmemenge. Taucht man den 80°C warmen und 100 g schweren Kupferklotz in 500 g Wasser, welches 20 °C warm ist und wartet eine geringe Zeit, so haben beide Stoffe anschließend 21,1 °C.
Vorher:

Nachher:

- Temperaturausgleich beim Berühren;
- Die Wärmenergie fließt so lange von der warmen Stoffportion in die kältere, bis beide dieselbe Temperatur haben.
b) Zusammenhang zwischen Q, m und ΔT
Wie ändert sich eigentlich die Temperatur, wenn man immer die gleiche Masse unterschiedlicher Metalle mit gleicher Temperatur nimmt.
Vorher:
Wichtiger Hinweis: In dieser Abbildung ist mir ein Fehler unterlaufen. Die Temperatur des Wassers muss 20 °C betragen!

Nachher:
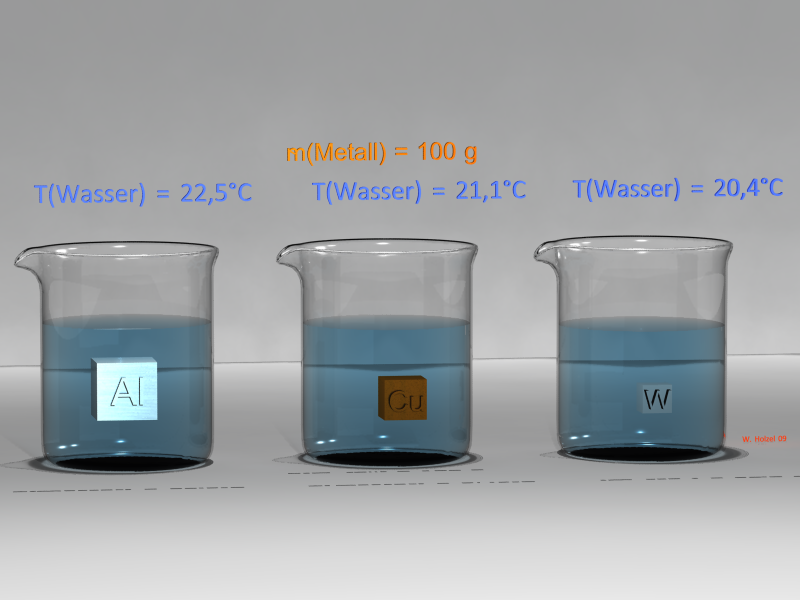
- Wärme und Temperatur sind unterschiedliche Dinge. Wären sie das Gleiche, wären die Mischungstemperaturen auch gleich.
- Die drei Würfel enthalten unterschiedliche Wärmemengen.
c) Zusammenhang zwischen Q, n (Stoffmenge) und ΔT
Vorher

Nachher

- Gleiche Stoffmengen transportieren bei Metallen die gleiche Wärmemenge.
d) Zusammenhang zwischen Q, n (Stoffmenge), Teilchenart und ΔT
Vorher:

Nachher:

- Die Wärmemenge und die Wärmekapazität Cp [= Wärmespeichervermögen] (auch die molare) sind von den verschiedenen Teilchenarten ab.
Spezifische Wärme einer Substanz ist die Wärmemenge, die benötigt wird, um 1 g der Substanz um 1 °C zu erwärmen.
Oder: Die Wärmekapazität gibt an, wie viel thermische Energie ein Körper bezogen auf die Temperaturänderung speichern kann:
Wärme Q ist direkt proportional der Temperaturänderung:
Qp ~ ΔT
Proportionalitätsfaktor für ein System = Wärmekapazität C:
Qp = C ⋅ ΔT
Für eine bestimmte Temperaturänderung ist umso mehr Wärme erforderlich, je größer die Masse m des Systems ist
Qp ~ m ⋅ ΔT
spezifische Wärmekapazität c (Wärmekapazität bezogen auf die Masse):
c = C/m ⇔ C = c ∙ m
Qp = c ⋅ m ⋅ ΔT
Molare Wärmekapazität Cm (bezogen auf die Stoffmenge n)
Cm = C/n ⇔ C = Cm ∙ n
Qp = Cm ∙ n ⋅ ΔT
Spezifische Wärmemenge c eines Stoffe: entspricht der Wärme Q, die zur Erwärmung von 1 g dieses Stoffes um 1 K bei konstantem Druck auf diesen Stoff übertragen werden muss.
Bsp.: cp(Wasser) = 4,184 J • g⁻¹ • K⁻¹
Frage: Welche Wärmeenergie wird benötigt, um 125 g Wasser von 20°C auf 25°C zu erwärmen?
Lösung:
Qp = cp ⋅ m ⋅ ΔT = 4,184 J • g⁻¹ • K⁻¹ ⋅ 125 g ⋅ 5 K = 2615 J = 2,615 kJ
=> Wärmekapazität von Wasser ist wichtig, um andere Reaktionsenthalpien messen zu können.
